Преобразование панорам в фотопланы.

Панорамы лунных и венерианских станций получены при помощи оптико-механических сканнеров (ОМС), с принципом действия которых можно ознакомиться в соответствующем разделе .

Переданное изображение отличается большой информационной насыщенностью, но страдает некоторыми характерными искажениями, мешающими правильному интуитивному восприятию панорамы в целом (в частности, возникает ощущение, что станция находится на локальной возвышенности). Неизбежность подобных искажений станет понятной, если мы укажем на практически круговой охват панорам.

Для удобства работы с панорамой ОМС удобно иметь на руках некое вспомогательное изображение (фотоплан), помогающий осуществлять привязку деталей панорамы к местности.

Здесь будет дан способ построения простейшего фотоплана, приведена программа для соответствующей конверсии и дан пример обработки панорамы. В качестве примера будет использована третья панорама АМС "Луна-13":

При построении простейшего фотоплана мы будем предполагать, что неровности рельефа невелики. Нашей задачей является конверсия исходного изображения в фотоплан, изображающий в определенном масштабе окрестности места посадки. В 60-х годах такое преобразование делалось аналоговыми средствами. Использование компьютера, естественно, обеспечивает большую точность и гибкость.

Геометрия съемки АМС "Луна-9, 13" дается следующей схемой:

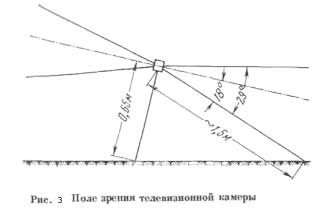
Естественно, если положение АМС после посадки не вполне ровное, соответствующие длины и углы должны быть пересчитаны и заменены на эквивалентные.

Нетрудно видеть, что лучи, выходящие из телефотометра под определенными углами, образуют при вращении семейство соосных круговых конусов. В сечении этого семейства конусов плоскостью наблюдения мы будем иметь, как известно из теории конических сечений, два семейства гипербол, разделенных прямой (соответствующей выходу нормального луча). В нижней полуплоскости при достаточно больших углах сканирования мы можем также иметь семейство эллипсов.

Эти линии на плоскости соответствуют горизонталям на панораме.

Вертикали на панораме соответствуют на плоскости наблюдения семейству прямых, проходящих через основание телефотометра. Общая картина дается следующей схемой:

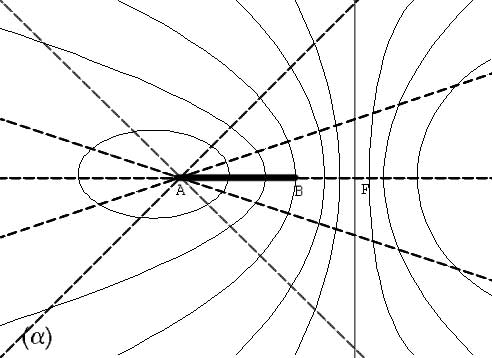
В случае строго вертикального или горизонтального расположения телефотометра картина упрощается. Вертикальному расположению соответствует семейство окружностей, пересеченных радиально расходящимися прямыми. Горизонтальному -- семейство параллельных прямых, пересекающих правые (левые) ветви гипербол. Эти два случая не имеют непосредственного интереса в рамках данного рассмотрения.

Формулу для преобразования координат легко можно получить методами "школьной" геометрии из рассмотрения следующего построения:

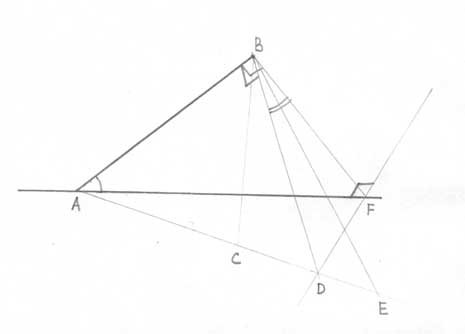
В связи с тривиальностью она приводится ниже без вывода:

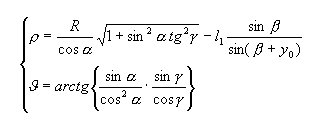
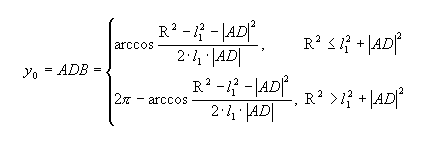
Здесь R=|AB| -- длина основания камеры, α=BAF -- наклон камеры к плоскости наблюдения, γ=FBD -- угол поворота телефотометра, ρ и θ -- координаты наблюдаемой точки в полярной системе координат, β=DBC -- вертикальный угол сканирования, отсчитывемый вниз от нормальной линии.

Та же формула верна и при углах сканирования γ>π/2. Нужно лишь осуществить замену:

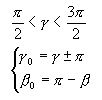
Указанная формула не работает при строго вертикальном и строго горизонтальном расположении телефотометра, а также в окрестности γ≈π/2.

Угол y₀ при данном угле поврота γ соответствует вертикальному углу сканирования β, при котором луч достигает горизонта.

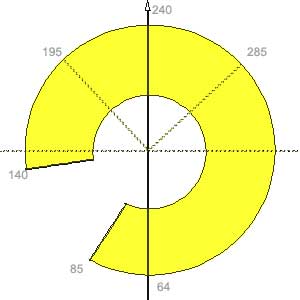
При правильной посадке АМС на равнину ход линии горизонта на панораме дается следующей линией:

Сравнивая реальную линию горизонта с расчитаной теоретически, можно определить эффективные значения для R и α. Для этого можно использовать, например, простой Maple Worksheet .

При ровной посадке панорама должна выходить на горизонт при данной геометрии съемки при углах сканирования порядка 45°, что мы и наблюдаем на самом деле. Это свидетельствует о том, что станция села плашмя и ближайшая ее окрестность представляет собой достаточно ровную поверхность.

Вместе с тем на краях панорамы линия горизонта несколько выше расчетной, что говорит о том, что местность позади станции постепенно начинает подниматься.

Здесь можно скачать программу , реализующую указанное преобразование (EXE & source code for MSVC 6.0).

Третья панорама, которую мы рассматриваем, в исходном виде почти круговая:

Ниже приведена серия построенных по этой панораме фотопланов в последовательно уменьшающемся масштабе:

1:200

1:100

1:50

1:12